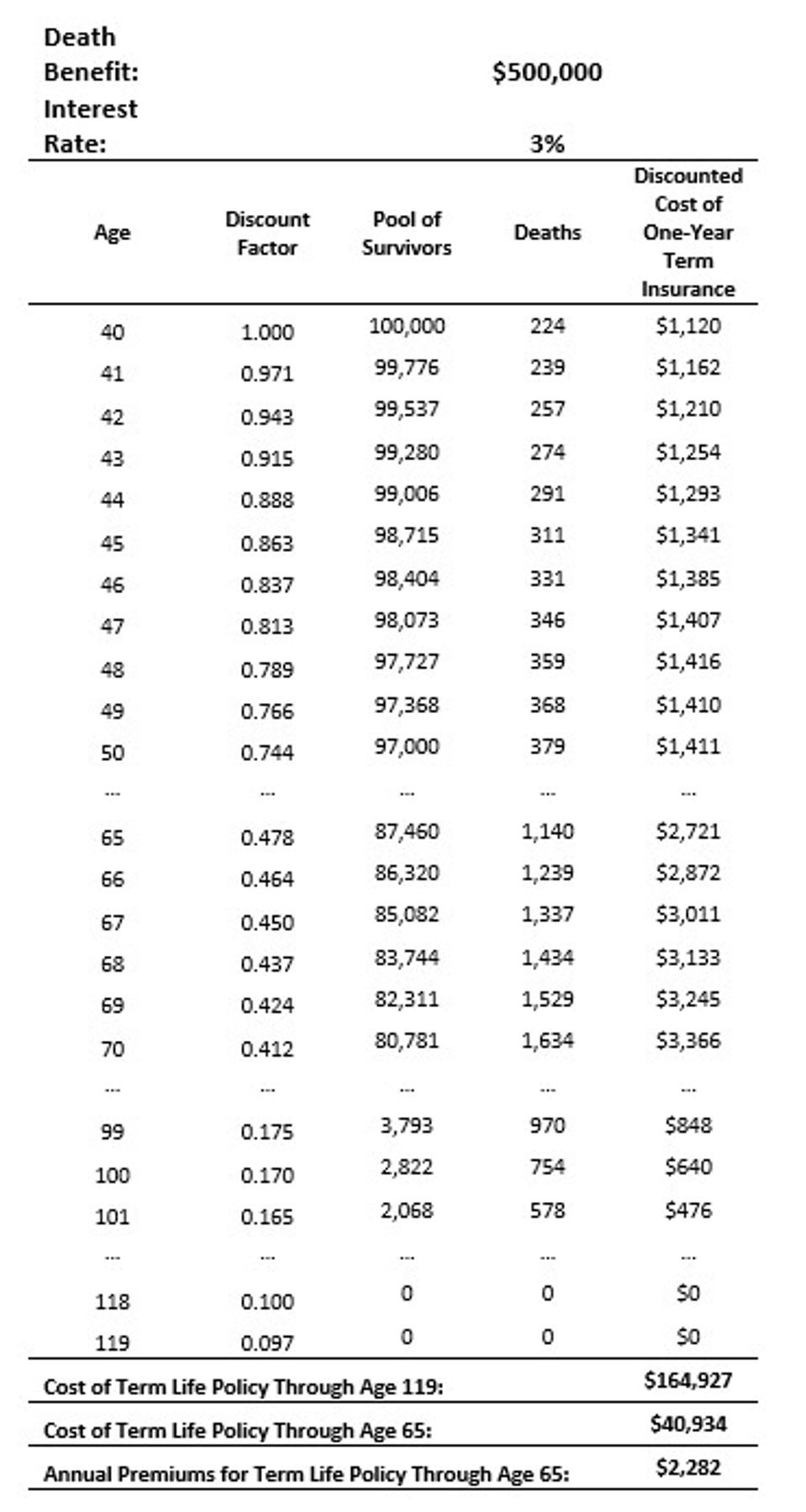
The way to understand how premiums are calculated on a term life insurance policy is to recognize that term life insurance is a collection of renewable one-year term policies. Consider that I buy a one-year term policy as a forty-year-old male. Given the mortality data I am using, the insurance company projects that over the next year, 224 forty-year-old males out of 100,000 will die, and this is the number of death benefits that must be paid. The insurance company must collect enough premiums to support these claims. For the population of 100,000 policy holders, this requires charging each participant $1,120 for their one-year of protection providing a $500,000 death benefit to those who die.
Next, suppose I seek protection for two-years instead of one. I still buy the policy at age forty, but I now wish to calculate the cost of protection at age forty-one as well. At age forty, I effectively buy a one-year policy that allows me to renew for the second year without going through additional underwriting. Mortality rates increase with age. But the insurance costs this implies will be partly offset by the fact that there is a smaller pool of survivors from the original pool of policyholders to which the increased mortality rates apply. Of the original 100,000 policy holders, 999,776 remain alive at forty-one and a further 239 of them are expected to die. The life insurance company must collect enough premiums to support these claims. Calculating the premium required today means looking at this cost of insurance in one year, but then further discounting the cost of insurance by the fact that by collecting premiums today, the insurance company can grow that money at the 3 percent rate for one year before it is needed to pay claims. With this discounting, the premium is $1,162. This process continues at each age that coverage is provided. Though not all ages are shown to conserve space, age eighty-seven is the year that the highest number of original policy holders (3,794) are expected to die. Even though mortality rates continue to grow with age, applying them to a dwindling pool of survivors means that the overall number of deaths subsequently declines. At age 100, 754 of the original policy holders are expected to die. The cost of insuring against death between the 100th and 101st birthdays is $640, reflecting the number of deaths among the original policyholders at that age as well as the discounting for the premium paid today that grows at 3 percent for many years before it is used to pay for those death benefit claims.
getty
Summing these insurance costs through age 119, the cost of providing a $500,000 death benefit is $164,927 if paid as a single premium today. This is reflecting the power of compounding interest as well as the role of risk pooling. Death is certain to happen at some point; paying $164,927 today would ensure a death benefit of $500,000 will be paid when death happens. Naturally, the sooner death happens, the higher would be the implied rate of return earned by the policy holder.
Though it is conceivable to buy a permanent term insurance policy as just described, this is not typically how most people approach term insurance. Instead, a term policy may be used in a temporary manner to protect human capital. The cost of a policy, then, is simply the cumulative costs of those one-year term policies for as long as coverage will be maintained.
Consider the case in which someone wishes to have the death benefit protection until reaching an anticipated retirement age of sixty-five. With insurance coverage ending on the 65th birthday, the cost is the sum of the twenty-five one-year policies from age forty through sixty-four. This cost is $40,934. The forty-year-old male could pay this amount today to receive the protection of $500,000 should death happen before age sixty-five. We can gather from the pool of survivors that 87,460 out of 100,000 would still be alive at sixty-five, and so 12,540 members of the pool would have received the death benefit by that time. The premiums of the survivors subsidize the death benefit payments for those who did not make it. This is risk pooling and mortality credits in the life insurance context.
MORE FOR YOU
One final matter to consider is that most people do not use this single premium payment method to pay for the term policy. Policyholders typically wish to spread those payments over time. How much should the insurance company charge as an annual premium to cover this term life policy through age sixty-five? To determine this, we can view the shift from a single premium to ongoing premiums as a loan provided by the insurance company to the policy holder. The insurance company needs $40,934 today to fund the term policy expiring at age sixty-five. In effect, the company provides a loan of this amount to the policyholder, and the policyholder pays back the loan over time in the form of annual premium payments. Assuming that the insurance company uses the same 3 percent interest rate for this calculation and that premiums are paid at the start of the year, the matter is to determine the annual premium needed to repay this loan. An annual premium of $2,282 is the solution to this PMT equation:
= PMT (3%, 25 years, -$40,934, $0)
Exhibit 7.1 Pricing a Term Life Insurance Policy for a Forty-Year-Old Male
Retirement Researcher
Regarding taxes, premium payments are made with after-tax dollars and the death benefit is received on a tax-free basis. This taxation structure for term life insurance is most similar to Roth IRAs as gains within the policy resulting from the death benefit being larger than the cumulative premiums paid are not taxed.
If one is thinking about term life insurance, an important policy option to consider for an additional cost is a provision allowing the owner to later convert the policy to permanent life insurance. This option would help to protect from the risk that one later determines a need for additional life insurance coverage but has also incurred a health problem causing him or her to no longer qualify for a new life insurance policy. Such conversion options generally will last for a fixed period or until a particular age.
*This is an excerpt from Wade Pfau’s book, Safety-First Retirement Planning: An Integrated Approach for a Worry-Free Retirement. (The Retirement Researcher’s Guide Series), available now on Amazon
AMZN
